Projects & Initiatives
Easy as π
They say the best way to learn math is by practicing problems over and over again. What if we could generate these problems on-demand? This is the premise of this project: to provide students with an endless supply of math problems.
With Easy as π, we wanted to create a mobile application that could:
- Generates arithmetic problems at various levels of difficulty
- Selects the correct level of difficulty of problem to display to a student
We completed this project in a team of 4 students as part of a software engineering course at the University of British Columbia. While the focus of the course was on the engineering aspect of software development (software architecture, scope, testing, etc.), we still took the opportunity to conduct user research prior to beginning development of this mobile app.
Understanding our potential users
This app has two primary groups of users, students and teachers, which have different set of needs. Given these groups, we created several personas for each group based on our initial online research and prior experience.
Ewen is a grade 3 student and loves video games. He can quickly get addicted to games on his parent's phones. He is not very interested in school and lags behing compared to his classmates.
Jess is a teacher in a class of 32 students. She struggles to find time to help all her students individually and she is worried that if she spent more time, the rest of her class would not do anything productive.
Pete is a consultant in an engineering firm and has difficulty coming home early most days of the week. He wants to make sure his son gets enough practice in mathematics to make sure he does well in school.He wants him to learn how to study on his own, but he doesn't know where to start and is often not around to help him.
From these personas, we brainstormed a list of potential needs and pain points for each group, which helped inform the design of the mobile app.
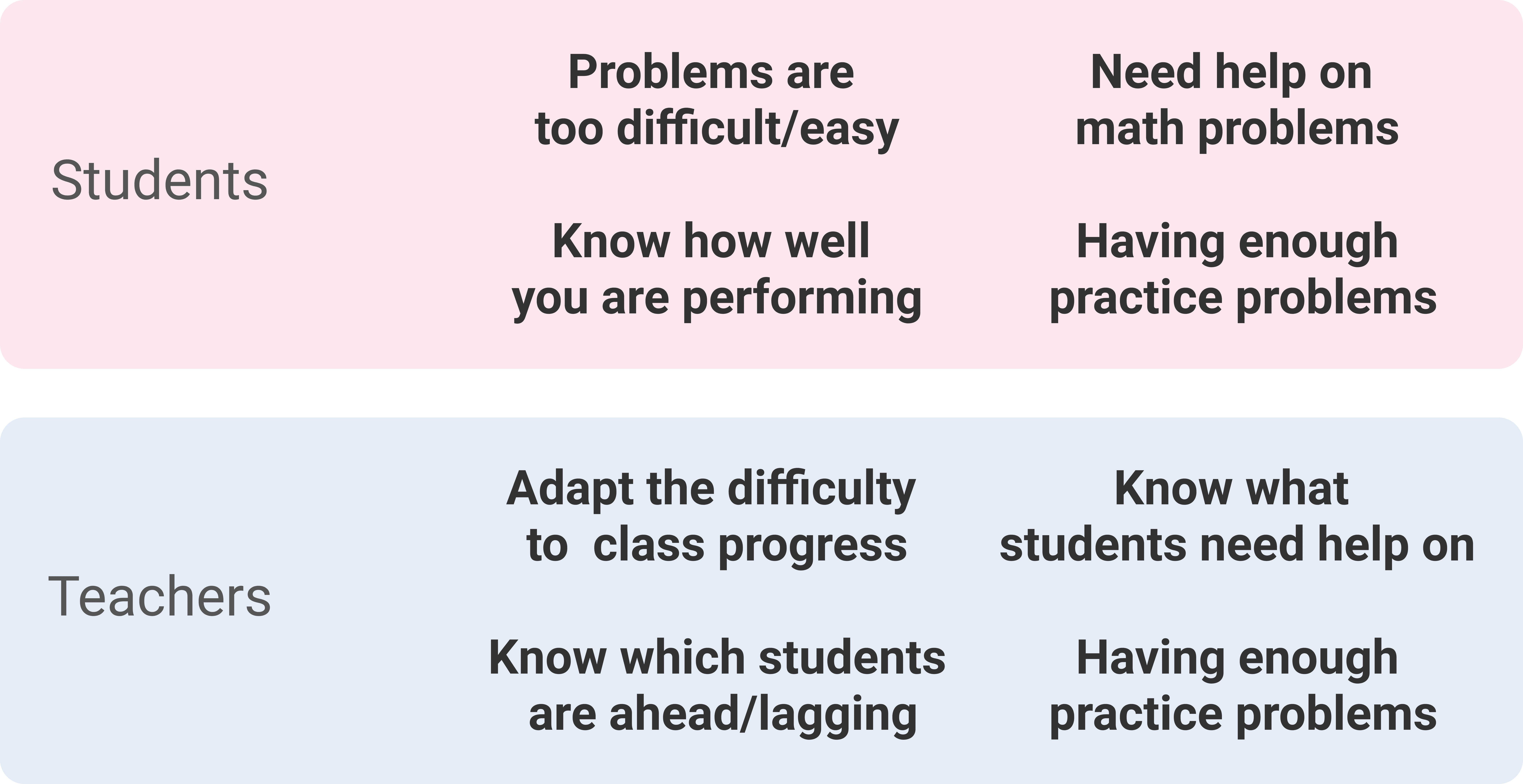
Based the on the user research above, we determined the following features our app should include:
Students
- Work on a daily math set
- Ask for help from their teacher
- Access learning material to solve a particular problem
- Track their success rate
Teachers
- Create a virtual classroom
- Prepare the content of the daily math set
- View individual student progress in each domain area
- Add recommended learning material
High-fidelity mockups
I was responsible for implementing the mobile app. I started by sketching a potential user flow for the authentication process and for the main features of the student app.
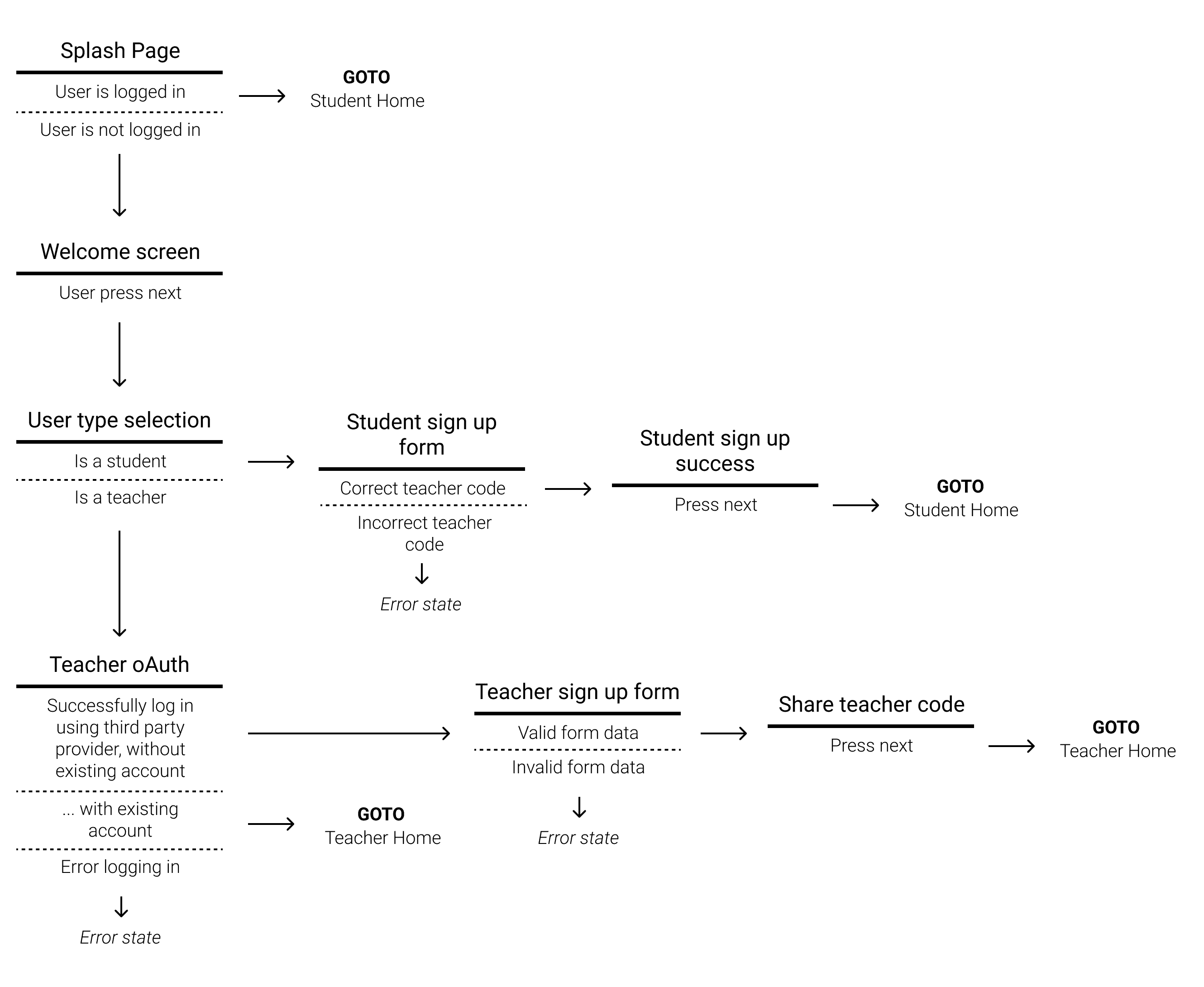
With these sketches in mind, I created a set of high-fidelity mockups in Figma that outlines various steps of the onboarding process for teachers and students, and the primary screens of the student app.
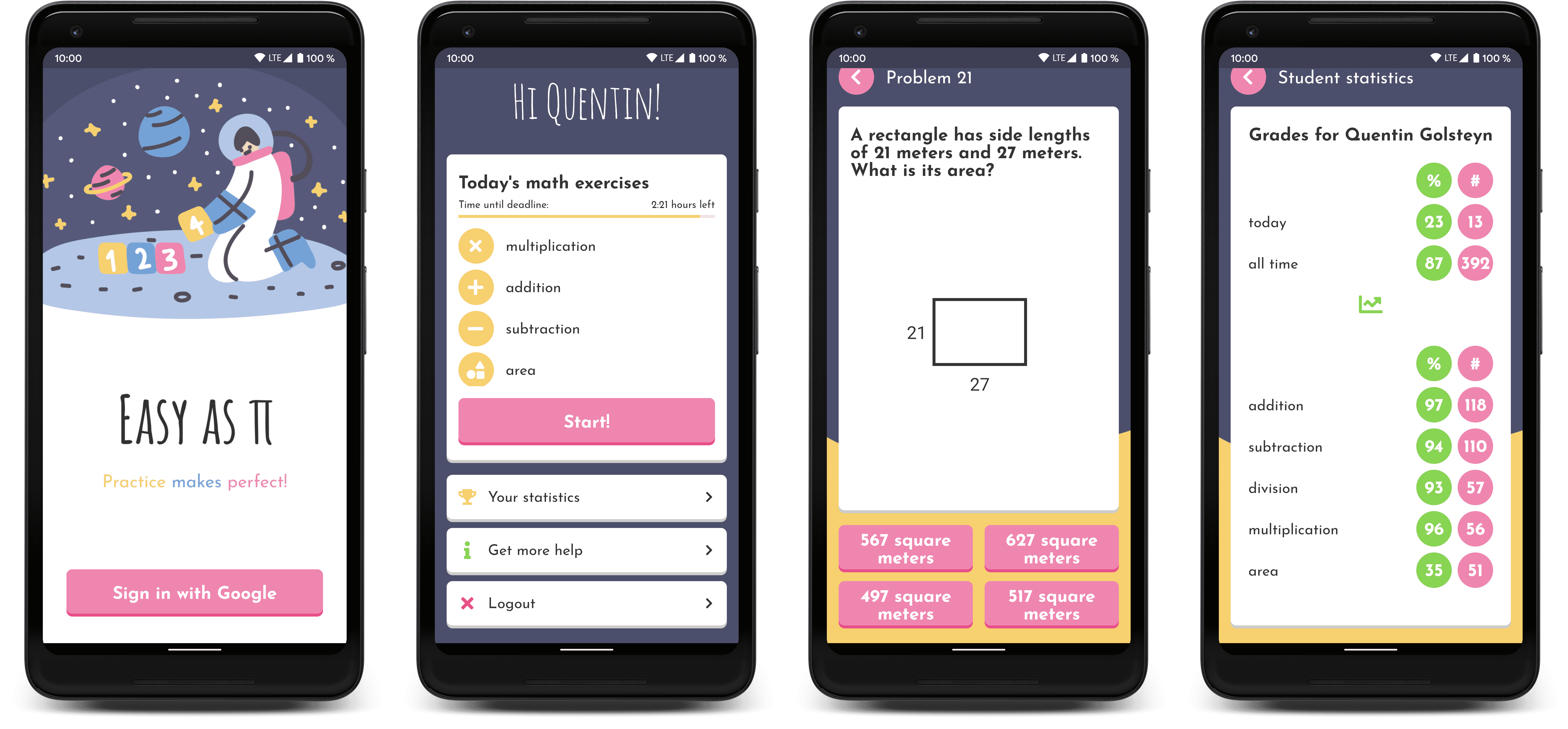
Given more time, we would have started with low-fidelity mockups to present to teachers and parents before proceeding with more time-intensive prototypes. Further iterations before starting development could have helped us get a better understanding of what needed to be implemented, and avoid some churn later down the road.
Implementation
We developed the mobile application in React Native, using the Expo library. The backend was an Node.js Express server using MongoDB for data storage. Authentication was done with Google OAuth.
Generating math problems
The BC math curriculum from grade 1 to 5 was essential for this project. It provides specific learning outcomes students should be able to achieve at each year level. For example, in Grade 1, students are expected to be able to add numbers up to 10.
To determine the correct problem to show the student, students are categorized according to their grade and their expertise within their grade. The rules selected to generate a problem of a particular type will vary depending on the student's assigned level. Each rule of a particular problem type can be formulated as a set of controlled and derived variables.
For example, for addition problems in Grade 1, students are expected to be able to add a "large" number with a "small" number to values up to 9. In this scenario, we can define two controlled variables, and and one derived variable, .
Controlled variables have their values bounded, for this example and . A random value within the appropriate domain is assigned to each controlled variable when generating a math problem. The derived variables have a value derived from the controlled variables, here .
With the variables defined, we can then specify a problem template and insert the variable values in the problem statement and answer. For our addition example, the problem statement could be Solve and the answer would be . With and , the generated problem would therefore be Solve and the answer would be .
Adapting to the student's performance
Depending on the student performance, we can adjust the category the student is in to vary the problems difficulty. Students score or lose points depending on whether they get problems right or wrong. Each level a student is in allows for a maximum of 10 points. If a students exceeds these 10 points, they "graduate" to the next category. If a students drops below zero point, they are demoted a level.
Students receive one point for each correct answer, and lose 2 points for each wrong answer. It is important to note, however, that these scores are given per problem type. A student may be "Grade 2 high" on addition, but "Grade 1 medium" on substraction.

